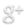Sierpinski-Dreieck
Ich habe kürzlich das Sierpinski-Dreieck für mich entdeckt, als ich einem Freund bei seinen Java-Aufgaben geholfen habe. Das Sierpinski-Dreieck ist ein Fraktal aus Dreiecken, die selbstähnlich sind, beschrieben von Waclaw Sierpinski, mehr dazu auf http://de.wikipedia.org/wiki/Sierpinski-Dreieck.
Ich dachte mir, dass muss doch auch für meinen kleinen Blog hier machbar sein, allerdings wollte ich kein JavaApplet haben. Auf http://www.walterzorn.de/jsgraphics/jsgraphics.htm habe ich eine JavaScript Bibliothek gefunden, mit der man mit Hilfe von farbigen DIV Containern malen kann, finde ich toll.
Diese habe ich dann auch benutzt, um das Sierpinski-Dreieck einmal in JavaScript zu implementieren.
Die Zeichnung besteht wirklich nur aus DIVs 🙂
Es folgt der JavaScript Code, den ich dazu geschrieben habe. Die Sierpinski Funktion war ursprünglich eine Java Methode aus einem Übungsblatt, die ich für JavaScript entsprechend angepasst habe.
Code Highlight von http://quickhighlighter.com
<div id="canvas" style="position:relative;width:100%;height:450px;">
</div>
<!-- hier beginnt das Java Script -->
<script id="js" type="text/javascript">
<!--
var jg = new jsGraphics("canvas"); //Variable für das Zeichenobjekt
function triangle(x1,y1,x2,y2,x3,y3) //Objektdefinition für das Dreieck, inklusive Konstruktor
{
//Variablen für Start- und Endpunkte sowie Kantenlänge und Flächeninhalt
this.x1=x1;
this.x2=x2;
this.x3=x3;
this.y1=y1;
this.y2=y2;
this.y3=y3;
this.a=0;
this.b=0;
this.c=0;
this.area=0;
//Kantenlängen und Flächeninhalt müssen berechnet werden
this.update();
}
//Setter
triangle.prototype.setx1 = function(x1){
this.x1=x1;
}
triangle.prototype.setx2 = function(x2){
this.x2=x2;
}
triangle.prototype.setx3 = function(x3){
this.x3=x3;
}
triangle.prototype.sety1 = function(y1){
this.y1=y1;
}
triangle.prototype.sety2 = function(y2){
this.y2=y2;
}
triangle.prototype.sety3 = function(y3){
this.y3=y3;
}
//Kantenlängen und Flächeninhalt neu berechnen
triangle.prototype.update = function(){
this.setA();
this.setB();
this.setC();
this.setArea();
}
//Berechnung der Kantenlängen nach dem Satz des Pythagoras
triangle.prototype.setA = function() {this.a = Math.sqrt((this.x2-this.x1)*(this.x2-this.x1)+(this.y2-this.y1)*(this.y2-this.y1));} //Länge eines Vektors a1,a2 ist Wurzel aus(a1*a1 + a2*a2), wobei a1 = this.x2-this.x1 ist usw.
triangle.prototype.setB = function() {this.b = Math.sqrt((this.x3-this.x2)*(this.x3-this.x2)+(this.y3-this.y2)*(this.y3-this.y2));}
triangle.prototype.setC = function() {this.c = Math.sqrt((this.x1-this.x3)*(this.x1-this.x3)+(this.y1-this.y3)*(this.y1-this.y3));}
//Berechnung des Flächeninhalts nach dem Satz des Heron
triangle.prototype.setArea = function()
{
this.area = 0.25*Math.sqrt((this.a+this.b+this.c)*(this.a+this.b-this.c)*(this.b+this.c-this.a)*(this.c+this.a-this.b));
}
//Verschiebung des Dreiecks um einen Vektor (v1,v2)
triangle.prototype.move = function(v1,v2)
{
this.x1 = this.x1+v1;
this.x2 = this.x2+v1;
this.x3 = this.x3+v1;
this.y1 = this.y1+v2;
this.y2 = this.y2+v2;
this.y3 = this.y3+v2;
}
//das aktuelle Dreieck wird gezeichnet
triangle.prototype.draw = function()
{
jg.drawLine(this.x1,this.y1,this.x2,this.y2);
jg.drawLine(this.x2,this.y2,this.x3,this.y3);
jg.drawLine(this.x3,this.y3,this.x1,this.y1);
jg.paint();
}
//die Sierpinski Funktion
function sierpinski(t)
{
t.draw();
if( t.area < 100 ) {
t.draw();
return;
}
t.setx2((t.x1+t.x2)/2);
t.sety2((t.y1+t.y2)/2);
t.setx3((t.x1+t.x3)/2);
t.sety3((t.y1+t.y3)/2);
t.move(t.x2-t.x1, t.y2-t.y1);
t.update();
sierpinski(t);
t.move(t.x3-t.x2, t.y3-t.y2);
t.update();
sierpinski(t);
t.move(t.x1-t.x3, t.y1-t.y3);
t.update();
sierpinski(t);
t.setx2(2*t.x2-t.x1);
t.sety2(2*t.y2-t.y1);
t.setx3(2*t.x3-t.x1);
t.sety3(2*t.y3-t.y1);
t.update();
}
//neues Dreieck erzeugen und nach Sierpinski zeichnen
var t1 = new triangle(0,0,500,0,250,433);
sierpinski(t1);
//-->
</script>